Lernauftrag 17: Gemischte Widerstände

Hier findest die Aufgaben ohne Lösungen.

In Versuch G5.0 - Reihenschaltung von Widerständen und G6.0 - Parallelschaltung von Widerständen haben wir die notwendigen Formeln kennengelernt um Widerstände zusammenzufassen und Spannungen und Ströme zu berechnen. (Siehe Tabellenbuch S.38)

Reihenschaltung

\(U_\mathrm{ges} = U_1+U_2+U_3+\ldots\)
\(I_\mathrm{ges}=I_1=I_2=I_3=\ldots\)
\(R_\mathrm{ges}=R_1+R_2+R_3+\ldots\)

Parallelschaltung

\(U_\mathrm{ges}=U_1=U_2=U_3=\ldots\)
\(I_\mathrm{ges} = I_1+I_2+I_3+\ldots\)
\(R_\mathrm{ges}=\frac{1}{\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\ldots}\)
Sonderfall bei zwei parallelen Widerständen
\(R_{1||2}=\frac{R_1\cdot R_2}{R_1+ R_2}\)

Aufgabe 1

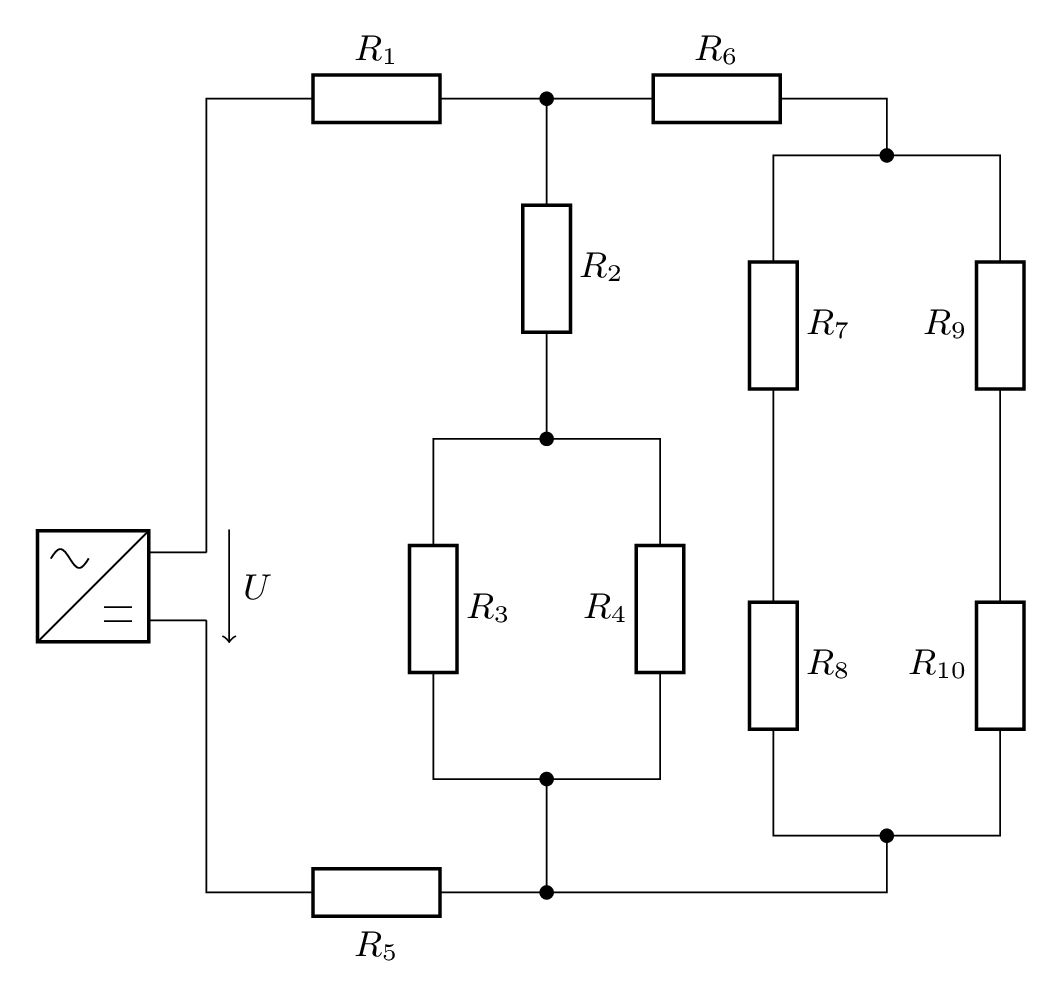
Zeichne zum Schaltbild alle Spannungs- und Strompfeile ein und berechne anschließend alle Werte mit folgenden vorgegebenen Werten:
geg:

\(U=12\ V\)
\(R_1=17\ \Omega\)
\(R_2=10\ \Omega\)
\(R_3=48\ \Omega\)
\(R_4=24\ \Omega\)
\(R_5=220\ \Omega\)
\(R_6=22\ \Omega\)
\(R_7=5,6\ \Omega\)
\(R_8=1,2\ \Omega\)
\(R_9=3,3\ \Omega\)
\(R_{10}=1,8\ \Omega\)

ges:

\(R_\mathrm{ges}\)
Spannungen \(U, U_1, U_2, U_3, U_4, U_5, U_6,U_7,U_8,U_9,U_{10}\)
Ströme \(I_1, I_2, I_3, I_4, I_5, I_6, I_7, I_8, I_9, I_{10}\)

Tragen wir zuerst alle Strom- und Spannungspfeile ein und notieren und an den Widerständen die gegebenen Werte:

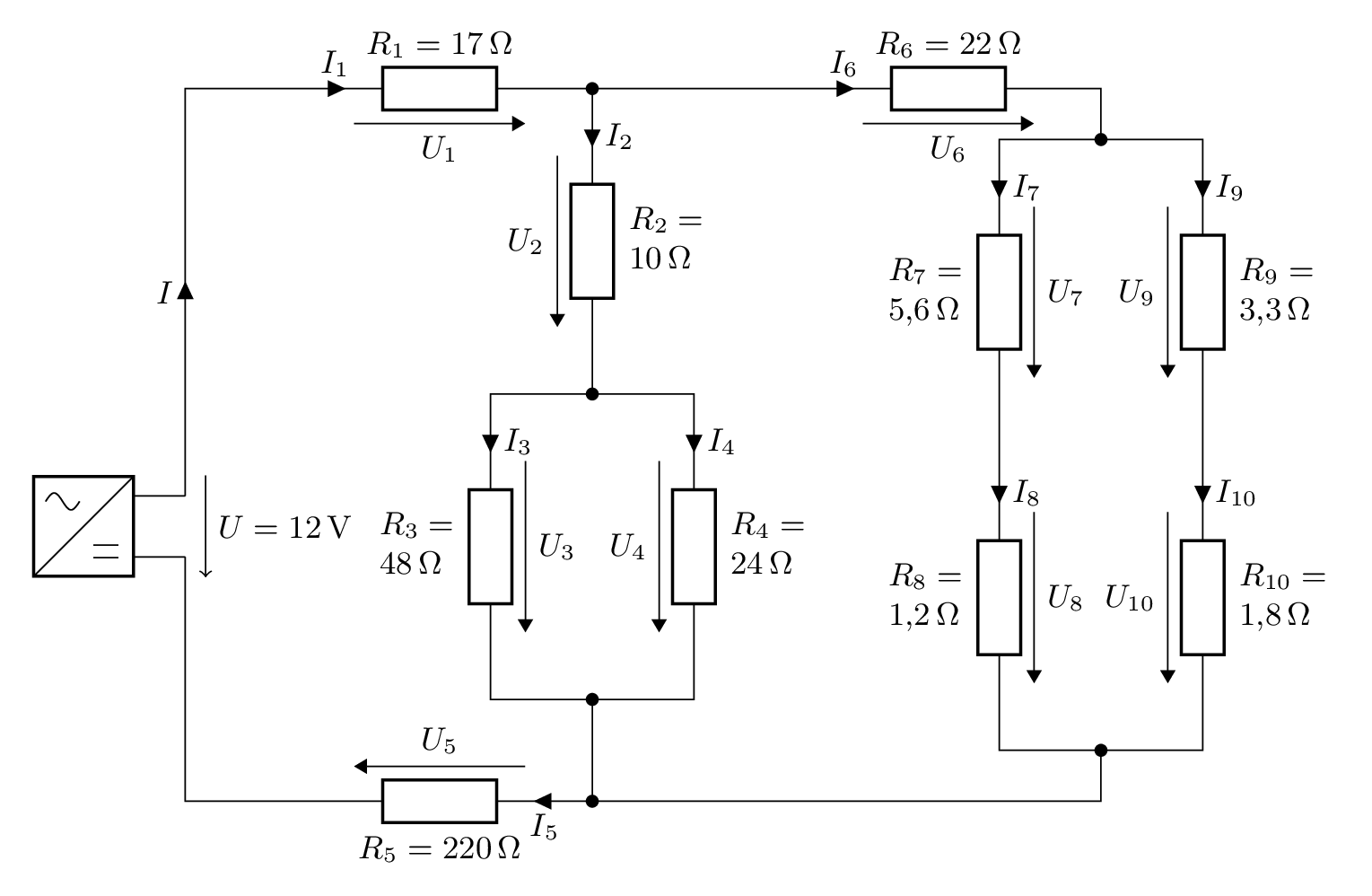
Ausgehend von dem Schaltbild halten wir erste Erkenntnisse aus dem Wissen über Reihen- und Parallelschaltungen fest. Folgende Ströme sind aufgrund von Reihenschaltung identisch:

\(I=I_1=I_5\)
\(I_7=I_8\)
\(I_9=I_{10}\)

Ferner sind folgende Spannung aufgrund von Parallelschaltung sicher identisch:

\(U_3 = U_4\)
\((U_7+U_8)=(U_9+U_{10})\Rightarrow\) Hier ist wichtig, daß nur die Summen der Spannungen identisch sind

Zusätzlich können wir für die Ströme festhalten, daß

\(I_1=I_2+I_6\Rightarrow\) der Strom teilt sich am Knoten auf
\(I_2=I_3+I_4\)
\(I_6=I_7+I_9\)

Im ersten Schritt fassen wir die parallelen Widerstände \(R_3\) und \(R_4\) (grün) und die in Reihe liegenden Widerständen \(R_7, R_8\) (blau) und \(R_9, R_{10}\) (rot) zusammen.

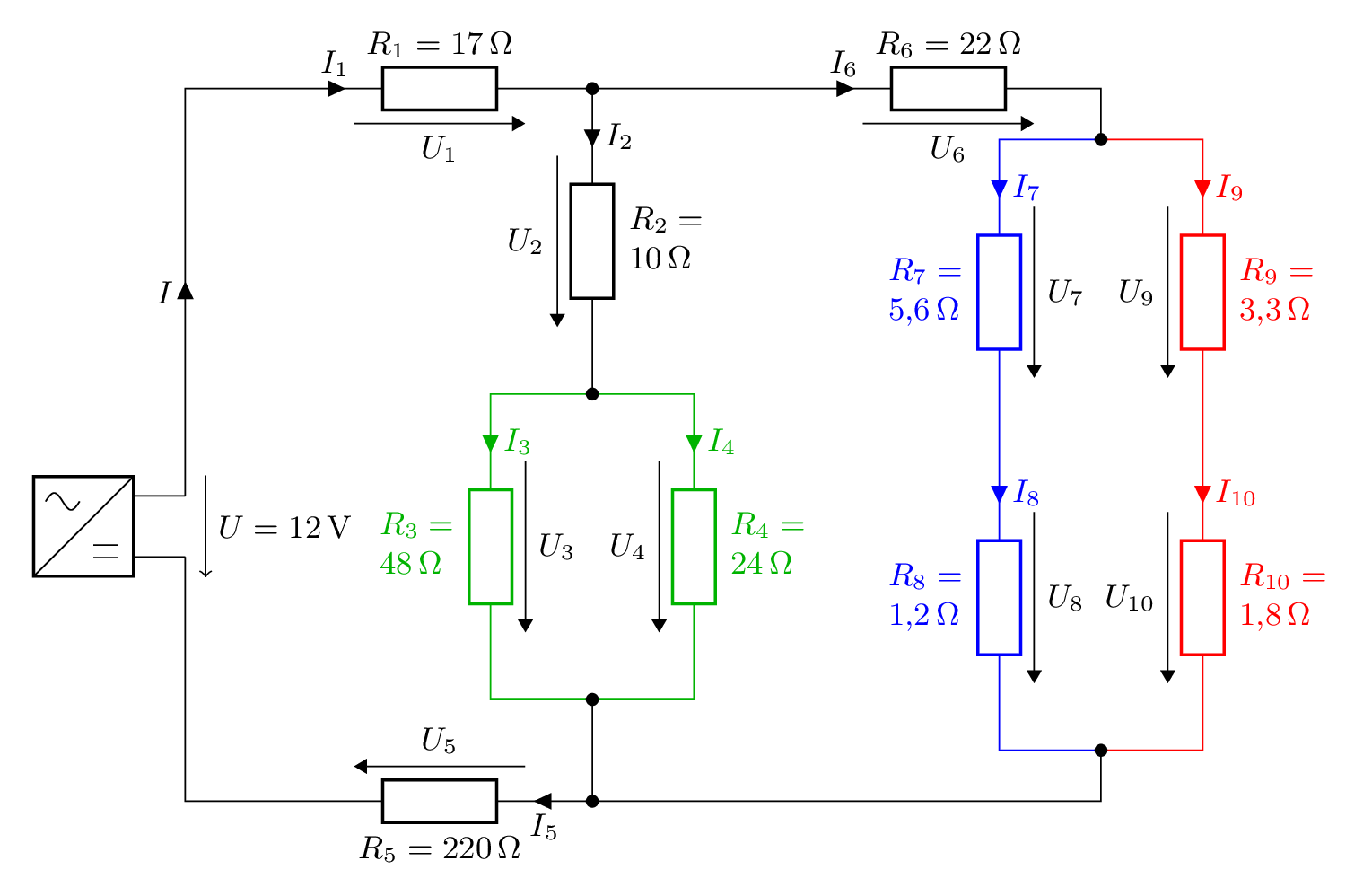
Damit wir Übersichtlichkeit im weiteren Verlauf bewahren können, werden wir die zusammengefassten Widerstände mit neuen Namen versehen und verwenden dafür Indizes, die bisher noch nicht verwendet wurden. Bisher verwendet waren die Indizes 1-10.
Also erhalten wir als Formeln:

\(R_{11}=R_{3||4}=\frac{R_3\cdot R_4}{R_3+R_4}=\frac{48\ \Omega\cdot24\ \Omega}{48\ \Omega+24\ \Omega}=16\ \Omega\)
\(R_{12}=R_{7+8}=R_7+R_8=5,6\ \Omega+1,2\ \Omega=6,8\ \Omega\)
\(R_{13}=R_{9+10}=R_9+R_{10}=3,3\ \Omega+1,8\ \Omega=5,1\ \Omega\)

und erhalten folgendes Schaltbild:

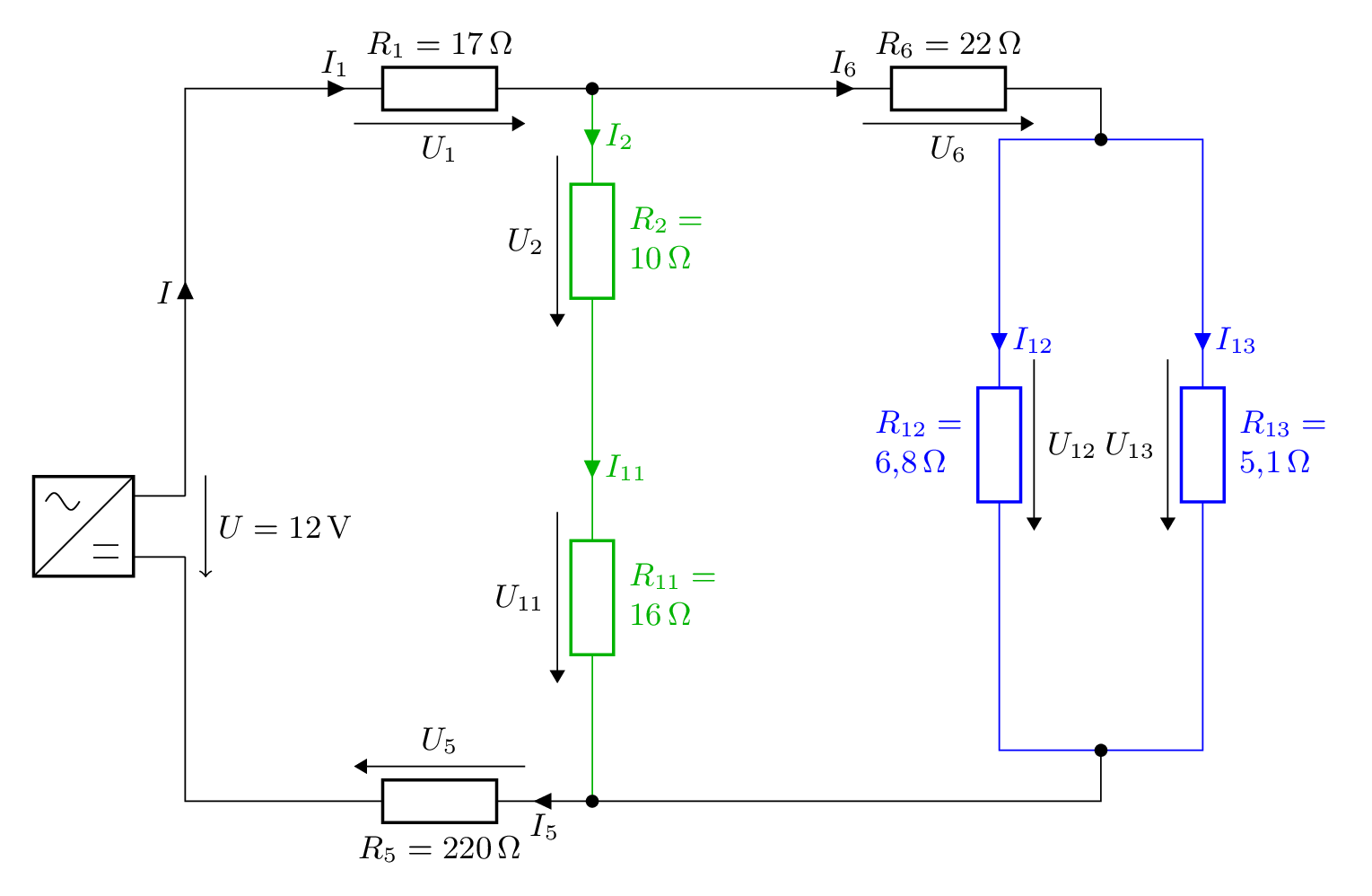
Halten wir an dieser Stelle fest, daß folgende Ströme gleich sind:

\(I_2=I_{11}\)
\(I_{12}=I_7=I_8\)
\(I_{13}=I_9=I_{10}\)

und die Spannungen \(U_{12}\) ist gleich der Spannung \(U_{13}\).

Hier fassen wir nun die in Reihe liegenden Widerstände \(R_2, R_{11}\) (grün) und die parallelen Widerstände \(R_{12}, R_{13}\) (blau) zusammen und erhalten als Formeln:

\(R_{14}=R_{2+(11)} =10\ \Omega+16\ \Omega=26\ \Omega\)
\(R_{15}=R_{12||13}=\frac{R_{12}\cdot R_{13}}{R_{12}+R_{13}}=\frac{6,8\ \Omega\cdot5,1\ \Omega}{6,8\ \Omega+5,1\ \Omega}=2,91\ \Omega\)

und erhalten folgendes Schaltbild:

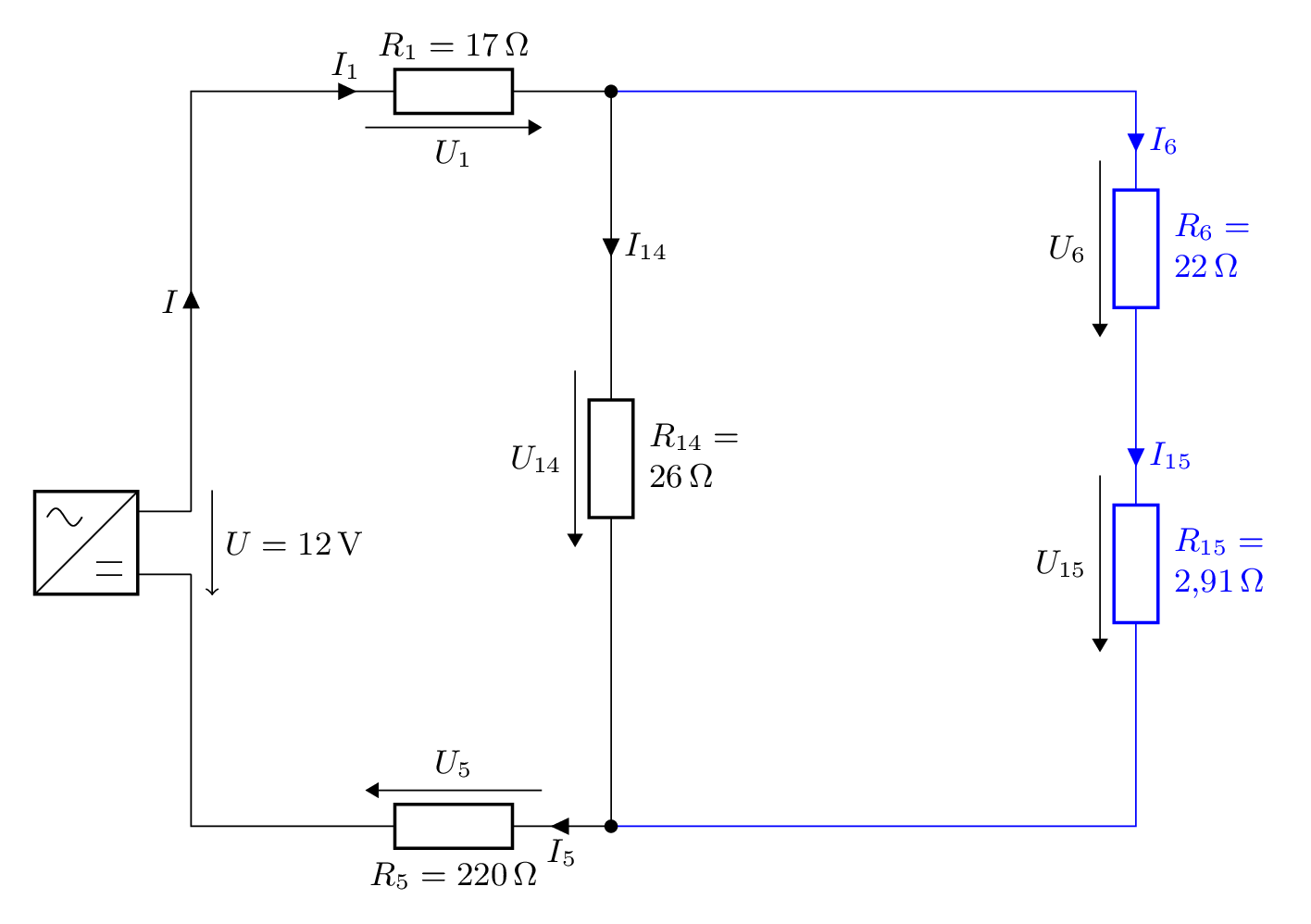
Wie zuvor halten wir zuerst gleiche Ströme und Spannungen fest

\(I_6=I_{15}\)
\(U_{14}=U_6+U_{15}\)

und fassen dann die in Reihe liegenden Widerstände \(R_6\) und \(R_{15}\) (blau) zusammen und erhalten als Formel:

\(R_{16}=R_{6+15}=22\ \Omega+2,91\ \Omega=24,91\ \Omega\)

und erhalten folgendes Schaltbild:

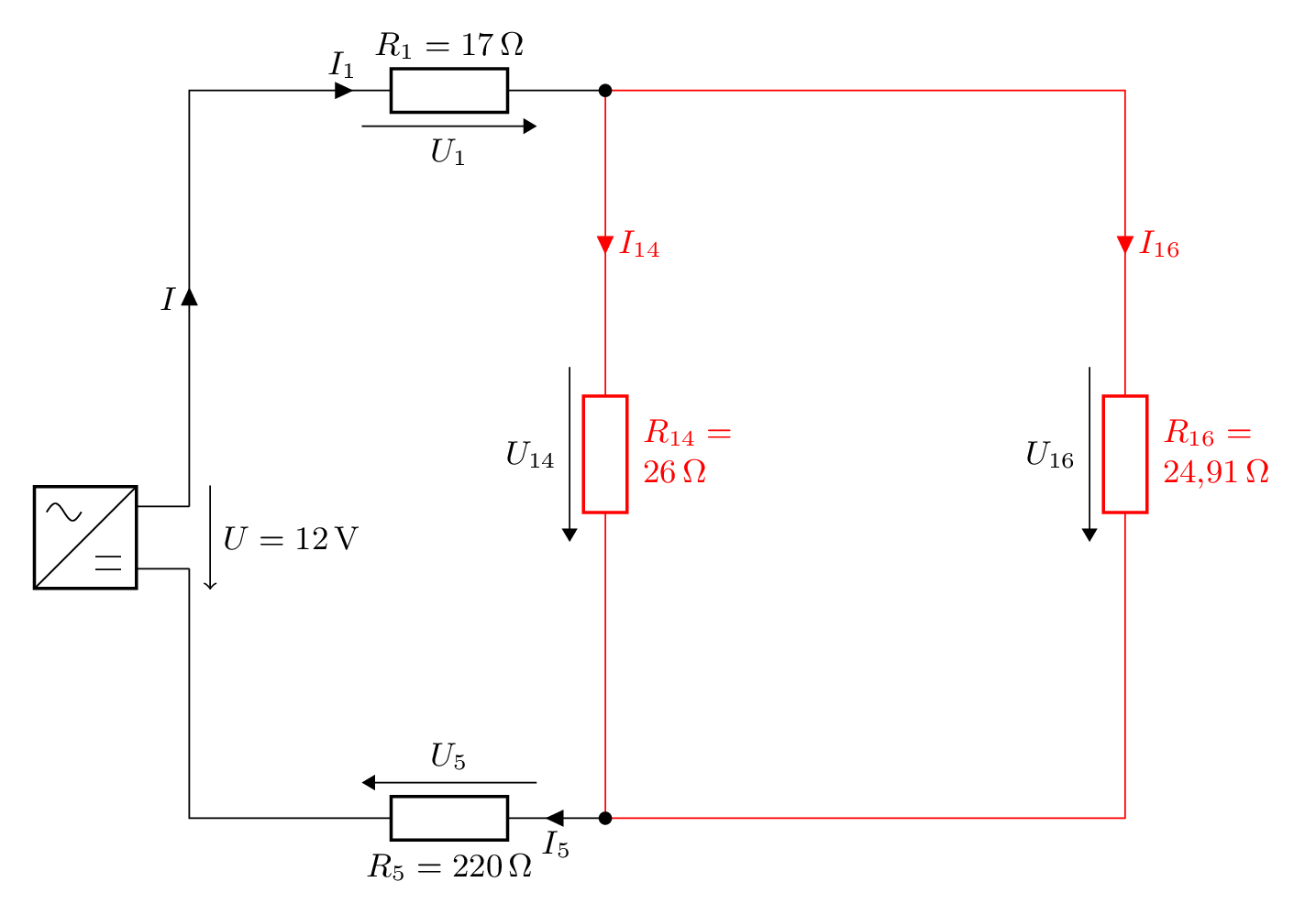
Es gilt

\(U_{14}=U_{16}\)
\(I_1=I_{14}+I_{16}\)

und wir fassen die parallelen Widerstände \(R_{14}\) und \(R_{16}\) (rot) zusammen und erhalten als Formel:

\(R_{17}=R_{14||16}=\frac{R_{14}\cdot R_{16}}{R_{14}+R_{16}}=\frac{26\ \Omega\cdot 24,91\ \Omega}{26\ \Omega+24,91\ \Omega}=12,72\ \Omega\)

und erhalten als Schaltbild

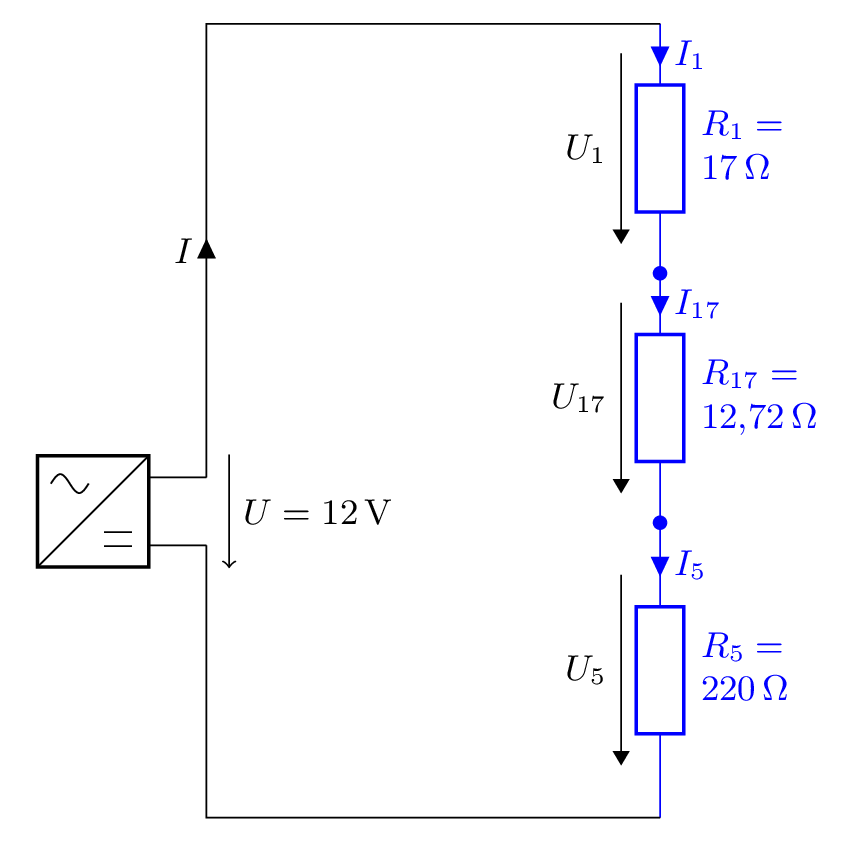
in welchem gilt

\(I_1=I_{17}=I_5\)

und wir schlußendlich die in Reihe liegenden Widerstände \(R_1\), \(R_{17}\) und \(R_5\) zusammenfassen und als Endformel erhalten
\(R_\mathrm{ges}=R_1+R_{17}+R_5=17\ \Omega+12,72\ \Omega+220\ \Omega=249,72\ \Omega\)

Von hier aus arbeiten wir uns Schritt für Schritt zurück. Wir kennen nun den Gesamtwiderstand \(R_{\mathrm{ges}}=249,72\ \Omega\) und die Gesamtspannung \(U=12\ V\) und können mithilfe des Ohmschen Gesetz den Strom \(I\) ausrechnen:
\(I=\frac{U}{R_{\mathrm{ges}}}=\frac{12\ V}{249,72\ \Omega}=0,04805\ A=48,05\ mA\)

Wir wissen nun mittlerweile, dass \(I=I_1=I_5\), ferner kennen wir die Werte für \(R_1\), \(R_5\), \(R_{17}\) und können mithilfe des Ohmschen Gesetzes die Spannungen \(U_1\), \(U_5\), \(U_{17}\) ausrechnen:
\(U_1=R_1\cdot I_1=R_1\cdot I= 17\ \Omega\cdot 0,04805\ A=0,81685\ V=816,85\ mV\)
\(U_5=R_5\cdot I_5=R_5\cdot I=220\ \Omega\cdot 0,04805\ A=10,57\ V\)
\(U_{17}=R_{17}\cdot I_{17}=R_{17}\cdot I=12,72\ \Omega\cdot 0,04805\ A=0,61119\ V=611,19\ mV\)

Nachdem wir die Spannungen \(U_1\) und \(U_5\) ausgerechnet hatten, hätten wir die Spannung \(U_{17}\) auch ohne das Ohmsche Gesetz berechnen können. In einer Reihenschaltung gilt:
\(U=U_1+U_{17}+U_5\)
Stellen wir dies auf \(U_{17}\) und erhalten
\(U_{17}=U-U_1-U_5=12\ V-0,81685\ V-10,57\ V=0,61315\ V=613,15\ mV\)

Schauen wir genau, so stellen wir fest, dass wir zwei unterschiedliche Werte für \(U_{17}\) errechnet haben. Das diese voneinander abweichen liegt an Rundungsfehlern, da wir uns darauf geeinigt haben Ergebnisse auf zwei Stellen nach dem Komma zu runden.
Im weiteren Verlauf verwenden wir den Wert: \(U_{17}=613,15\ mV\)

Wir kennen nun alle Werte für das Schaltbild:

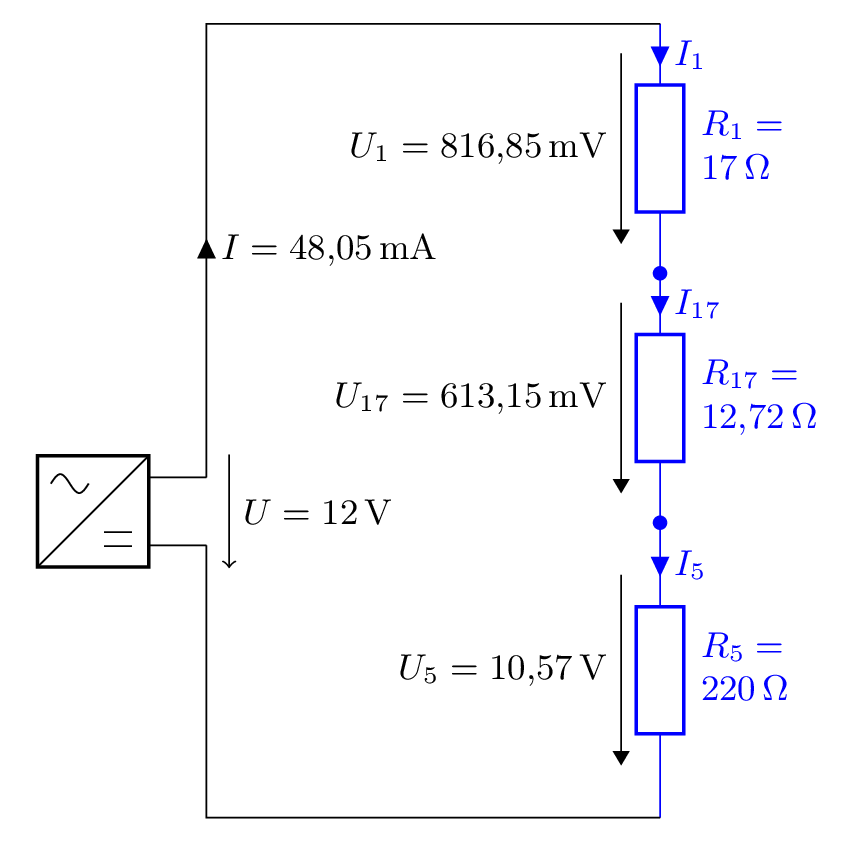
Nachdem wir die Spannung über den vereinten Widerstand \(R_{17}\) kennen, schauen wir, welche Zusammenfassung nötig war, um zu \(R_{17}\) zu kommen. Der Widerstand entstand aus zwei parallelen Widerständen. In parallelen Schaltungen ist die Spannung über alle parallelen Stränge identisch und es gilt:
\(U_{17}=U_{14}=U_{16}\)

Da wir Widerstandswerte für \(R_{14}\) und \(R_{16}\) bereits kennen, können wir die Ströme \(I_{14}\) und \(I_{16}\) mithilfe des Ohmschen Gesetzes bestimmen:
\(I_{14}=\frac{U_{14}}{R_{14}}=\frac{U_{17}}{R_{14}}=\frac{613,15\ mV}{26\ \Omega}=0,02358\ A=23,58\ mA\)
\(I_{16}=\frac{U_{16}}{R_{16}}=\frac{U_{17}}{R_{16}}=\frac{613,15\ mV}{24,91\ \Omega}=0,02461\ A=24,61\ mA\)

Nachdem wir den Strom \(I_{14}\) ausgerechnet hatten, hätten wir den Strom \(I_{16}\) auch ohne das Ohmsche Gesetz berechnen können. Für einen Knotenpunkt gilt, daß die einfließenden Ströme genauso groß wie die ausfließenden Ströme sind. In unserem Falle läßt sich das zusammenfassen als:
\(I=I_{14}+I_{16}\)
Stellen wir das auf \(I_{16}\) um, so erhalten wir
\(I_{16}=I-I_{14}=48,05\ mA-23,58\ mA=24,47\ mA\)
Auch hier stellen wir wieder fest, daß die berechneten Werte aufgrund von Rundungsfehlern voneinander abweichen.
Im weiteren Verlauf verwenden wir den Wert: \(I_{16}=24,47\ mA\)

Wir kennen nun alle Werte für folgenden Zustand:

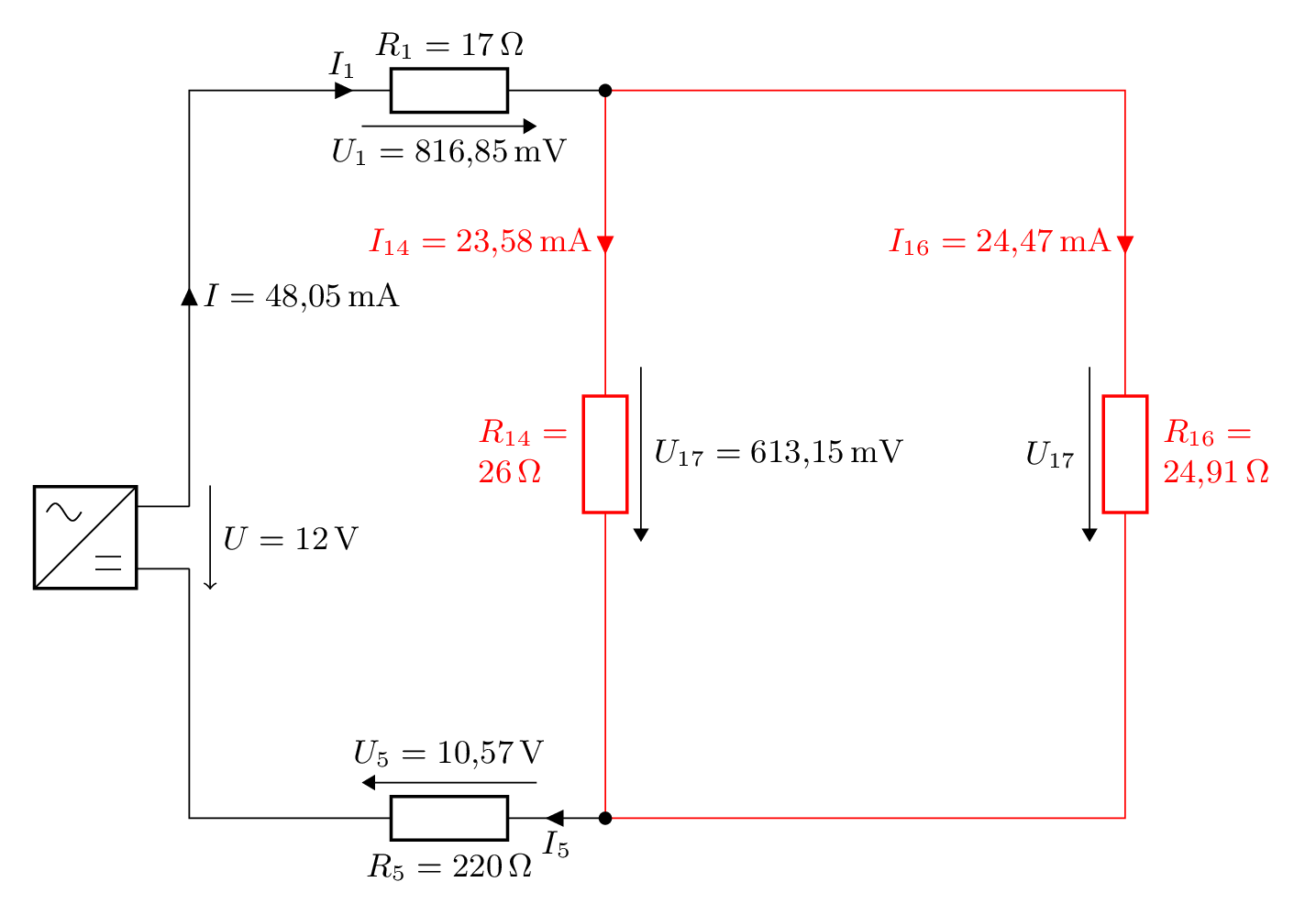
Hier ist günstig, nicht in beiden parallelen Strängen gleichzeitig zu arbeiten, sondern sich für einen zu entscheiden. Wir werden zuerst den Strang mit \(R_{14}\) auflösen und später den Strang mit \(R_{16}\) bearbeiten.

\(R_{14}\) entstand aus der Reihenschaltung von \(R_2\) und \(R_{11}\). In einer Reihenschaltung ist der Strom überall gleich, somit gilt: \(I_{14}=I_2=I_{11}\). Wir halten als Ergebnis fest: \(I_2=23,58\ mA\).
Mithilfe des Ohmschen Gesetzes, können wir nun die Spannungen \(U_2\) und \(U_{11}\) ausrechnen:
\(U_2=R_2\cdot I_2=R_2\cdot I_{14}=10\ \Omega\cdot 23,58\ mA=235,8\ mV\)
\(U_{11}=R_{11}\cdot I_{11}=R_{11}\cdot I_{14}=16\ \Omega\cdot 23,58\ mA=377,28\ mV\)

Nachdem wir \(U_2\) ausgerechnet hatten, hätten wir \(U_{11}\) auch ohne das Ohmsche Gesetz ausrechnen können. In der Reihenschaltung gilt
\(U_{17}=U_2+U_{11}\)
und stellen wir das auf \(U_{11}\) um, so erhalten wir
\(U_{11}=U_{17}-U_2=613,15\ mV-235,8\ mV=377,35\ mV\)

Erneut finden wir Rundungsabweichungen.

Im weiteren Verlauf verwenden wir den Wert: \(U_{11}=377,35\ mV\)

Der zusammengefasste Widerstand \(R_{11}\) entstand aus der Parallelschaltung der Widerstände \(R_3\) und \(R_4\). In einer Parallelschaltung gilt, dass die Spannungen über alle Stränge identisch ist und es gilt somit \(U_3=U_4=U_{11}\). Wir haben zwei weitere Ergebnisse gefunden, nämlich
\(U_3 = U_4 = 377,35\ mV\).

Mithilfe des Ohmschen Gesetzes können wir nun \(I_3\) und \(I_4\) ausrechnen:
\(I_3=\frac{U_3}{R_3}=\frac{U_11}{R_3}=\frac{377,35\ mV}{48\ \Omega}=0,00786\ A=7,86\ mA\)
\(I_4=\frac{U_4}{R_4}=\frac{U_11}{R_4}=\frac{377,35\ mV}{24\ \Omega}=0,01572\ A=15,72\ mA\)

Nachdem wir \(I_3\) ausgerechnet hatten, hätten wir \(I_4\) auch ohne das Ohmsche Gesetz ausrechnen können. Für einen Knotenpunkt gilt, daß die einfließenden Ströme genauso groß wie die ausfließenden Ströme sind. In unserem Falle läßt sich das zusammenfassen als:
\(I_2=I_3+I_4\)
Stellen wir das auf \(I_4\) um, so erhalten wir
\(I_4=I_2-I_3=23,58\ mA-7,86\ mA=15,72\ mA\)

Erfreulicherweise haben wir diesmal keine Rundungsfehler und sehen unser Ergebnis bestätigt.

Der Strang mit \(R_{14}\) ist somit erledigt und wir widmen uns dem Strang mit \(R_{16}\). Wir erinnern uns, dass galt \(U_{16}=U_{17}\).
\(R_{16}\) entstand aus der Reihenschalten von \(R_6\) und \(R_{15}\). In einer Reihenschaltung ist der Strom überall konstant und es gilt somit \(I_{16}=I_6=I_{15}\). Wir haben wieder einen Wert gefunden, nämlich \(I_6=24,47\ mA\).

Mithilfe des Ohmschen Gesetzes können wir die Spannungen \(U_6\) und \(U_{15}\) ausrechnen und erhalten:

\(U_6=R_6\cdot I_6=R_6\cdot I_{16}=22\ \Omega\cdot24,47\ mA=0,53834\ V=538,34\ mV\)
\(U_{15}=R_{15}\cdot I_{15}=R_{15}\cdot I_{16}=2,91\ \Omega\cdot24,47\ mA=0,07121\ V=71,21\ mV\)

Nachdem wir \(U_6\) ausgerechnet hatten, hätten wir \(U_{15}\) auch ohne das Ohmsche Gesetz ausrechnen können. In der Reihenschaltung gilt
\(U_{17}=U_6+U_{15}\)
und stellen wir dies auf \(U_{15}\) um, so erhalten wir
\(U_{15}=U_{17}-U_6=613,15\ mV-538,34\ mV=74,81\ mV\)
Hier finden sich wieder Abweichungen durch Rundungsfehler.
Im weiteren Verlauf verwenden wir den Wert: \(U_{15}=74,81\ mV\)

Der zusammengefasste Widerstand \(R_{15}\) entstand aus der Parallelschaltung der Widerstände \(R_{12}= 6,8\ \Omega\) und \(R_{13}=5,1\ \Omega\). In einer Parallelschaltung gilt, dass die Spannungen über alle Stränge identisch ist und es gilt somit \(U_{15}=U_{12}=U_{13}\).

Mithilfe des ohmschen Gesetzes können wir die Ströme \(I_{12}\) und \(I_{13}\) ausrechnen:
\(I_{12}=\frac{U_{12}}{R_{12}}=\frac{U_{15}}{R_{12}}=\frac{74,81\ mV}{6,8\ \Omega}=0,01100\ A=11\ mA\)
\(I_{13}=\frac{U_{13}}{R_{13}}=\frac{U_{15}}{R_{13}}=\frac{74,81\ mV}{5,1\ \Omega}=0,01467\ A=14,67\ mA\)

Nachdem wir den Strom \(I_{12}\) ausgerechnet hatten, hätten wir den Strom \(I_{13}\) auch ohne das Ohmsche Gesetz ausrechnen können. Für einen Knotenpunkt gilt, daß die einfließenden Ströme genauso groß wie die ausfließenden Ströme sind. In unserem Falle läßt sich das zusammenfassen als
\(I_{6}=I_{12}+I_{13}\)
und stellen wir das um auf \(I_{13}\) so erhalten wir
\(I_{13}=I_6-I_{12}=24,47\ mA-11\ mA=13,47\ mA\)
Erneut finden sich Abweichungen durch Rundungsfehler.
Im weiteren Verlauf verwenden wir den Wert: \(I_{13}=14,67\ mA\)

Der zusammengefasste Widerstand \(R_{12}\) entstand aus der Reihenschaltung von \(R_7\) und \(R_8\). In einer Reihenschaltung sind alle Ströme gleich und es gilt
\(I_{12}=I_7=I_8\).
Wir haben wieder zwei Werte gefunden, nämlich \(I_7=I_8=11\ mA\)

Mithilfe des Ohmschen Gesetzes können wir die Spannungen \(U_7\) und \(U_8\) ausrechnen
\(U_7=R_7\cdot I_7=R_7\cdot I_{12}=5,6\ \Omega\cdot 11\ mA=0,0616\ V=61,6\ mV\)
\(U_8=R_8\cdot I_8=R_8\cdot I_{12}=1,2\ \Omega\cdot 11\ mA=0,0132\ V=13,2\ mV\)

Nachdem wir \(U_7\) ausgerechnet hatten, hätten wir \(U_{8}\) auch ohne das Ohmsche Gesetz ausrechnen können. In der Reihenschaltung gilt
\(U_{15}=U_7+U_{8}\)
und stellen wir dies auf \(U_{8}\) um, so erhalten wir
\(U_{8}=U_{15}-U_7=74,81\ mV-61,6\ mV=13,21\ mV\)

Hier finden sich wieder Abweichungen durch Rundungsfehler und wir halten es Wert für \(U_{8}=13,21\ mV\) fest.

Der zusammengefasste Widerstand \(R_{13}\) entstand aus der Reihenschaltung von \(R_9\) und \(R_{10}\). In einer Reihenschaltung sind alle Ströme gleich und es gilt
\(I_{13}=I_9=I_{10}\)
Wir haben wieder zwei Werte gefunden, nämlich \(I_9=I_{10}=14,67\ mA\)

Mithilfe des Ohmschen Gesetzes können wir die Spannungen \(U_9\) und \(U_{10}\) ausrechnen
\(U_9=R_9\cdot I_9=R_9\cdot I_{13}=3,3\ \Omega\cdot 14,67\ mA=0,04841\ V=48,41\ mV\)
\(U_{10}=R_{10}\cdot I_{10}=R_{10}\cdot I_{13}=1,8\ \Omega\cdot 14,67\ mA=0,02641\ V=26,41\ mV\).

Nachdem wir \(U_9\) ausgerechnet hatten, hätten wir \(U_{10}\) auch ohne das Ohmsche Gesetz ausrechnen können. In der Reihenschaltung gilt
\(U_{15}=U_9+U_{10}\)
und stellen wir dies auf \(U_{10}\) um, so erhalten wir
\(U_{10}=U_{9}-U_6=74,81\ mV-48,41\ mV=26,40\ mV\)

Somit sind alle Werte berechnet.

Aufgabe 2

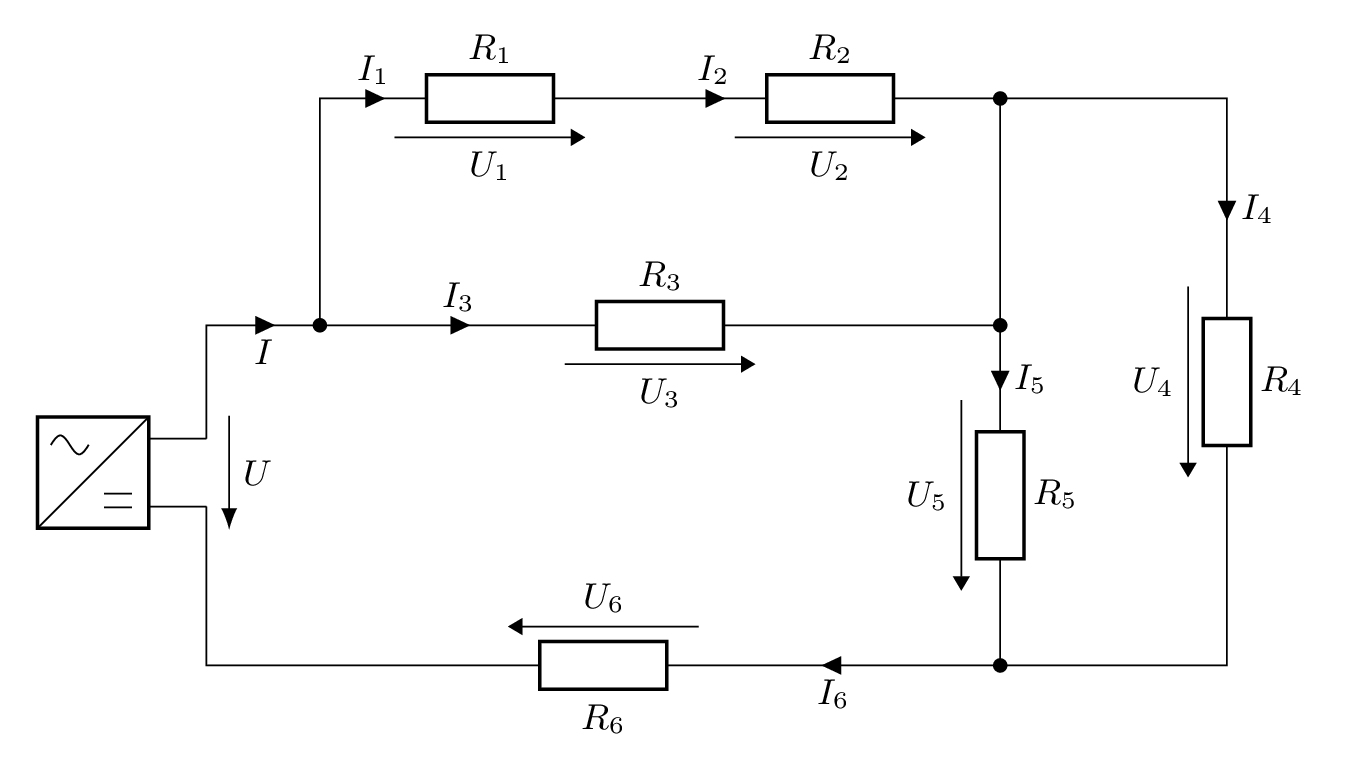
Notiere, welche Widerstände parallel zueinander sind und welche Widerstände in Reihe sind.
Arbeite dazu, wie im Beispiel, indem du schrittweise zusammenfasst und umzeichnest. Anschließend berechne die gesuchten Größen.
geg:

\(U=20\ V\)
\(R_1=220\ \Omega\)
\(R_2=330\ \Omega\)
\(R_3=680\ \Omega\)
\(R_4=100\ \Omega\)
\(R_5=220\ \Omega\)
\(R_6=47\ \Omega\)

ges:

\(R_\mathrm{ges}\)
Spannungen \(U, U_1, U_2, U_3, U_4, U_5, U_6\)
Ströme \(I_1, I_2, I_3, I_4, I_5, I_6\)

Lös:
\(R_7=R_1+R_2=550\ \Omega\)
\(R_8=R_7||R_3=304,07\ \Omega\)
\(R_9=R_4||R_5=68,75\ \Omega\)
\(R_\mathrm{ges}=R_8+R_9+R_6=304,07\ \Omega+68,75\ \Omega+47\ \Omega=419,82\ \Omega\)
\(I=\frac{U}{R_\mathrm{ges}}=\frac{20\ V}{419,82\ \Omega}=47,64\ mA\)
\(U_6=2,24\ V\)
\(U_9=3,28\ V=U_4=U_5\)
\(U_8=14,49\ V=U_3\)
\(I_4=32,8\ mA\)
\(I_5=14,91\ mA\)
\(I_3=21,31\ mA\)
\(I_7=26,35\ mA\)
\(U_1=5,80\ V\)
\(U_2=8,70\ V\)

Aufgabe 3

Notiere, welche Widerstände parallel zueinander sind und welche Widerstände in Reihe sind.
Arbeite dazu, wie im Beispiel, indem du schrittweise zusammenfasst und umzeichnest.

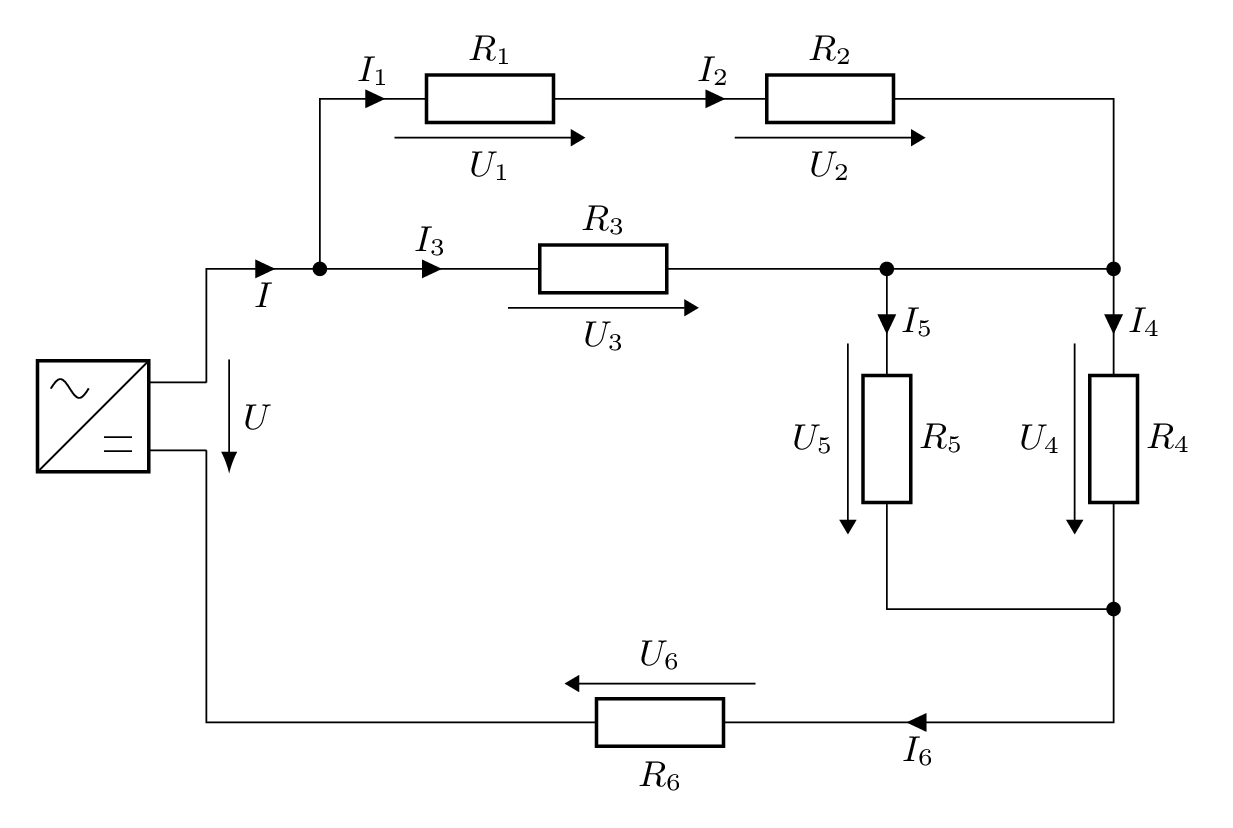
Notiere, welche Widerstände parallel zueinander sind und welche Widerstände in Reihe sind und berechne die gesuchten Größen.
geg:

\(I=12\ A\)
\(R_1=3\ M\Omega\)
\(R_2=12\ k\Omega\)
\(R_3=57\ m\Omega\)
\(R_4=47\ k\Omega\)
\(R_5=47\ \Omega\)
\(R_6=680\ \Omega\)

ges:

\(R_\mathrm{ges}\)
Spannungen \(U, U_1, U_2, U_3, U_4, U_5, U_6\)
Ströme \(I_1, I_2, I_3, I_4, I_5, I_6\)

Lös:
\(R_7=R_1+R_2=3012\ k\Omega\)
\(R_8=R_7||R_3=56,99\ m\Omega\)
\(R_9=R_4||R_5=46,95\ \Omega\)
\(R_\mathrm{ges}=R_8+R_9+R_6=56,99\ m\Omega+46,95\ \Omega+680\ \Omega=727,01\ \Omega\)
\(U=8724,12\ V\)
\(U_6=8160\ V\)
\(U_9=563,4\ V=U_4=U_5\)
\(U_8=683,88\ mV=U_3\)
\(I_4=11.99\ mA\)
\(I_5=11,99\ A\)
\(I_3=11.99\ A\)
\(I_7=227,05\ nA\)
\(U_1=36\ mV\)
\(U_2=144\ \mu V\)

Aufgabe 4

Notiere, welche Widerstände parallel zueinander sind und welche Widerstände in Reihe sind.
Arbeite dazu, wie im Beispiel, indem du schrittweise zusammenfasst und umzeichnest.

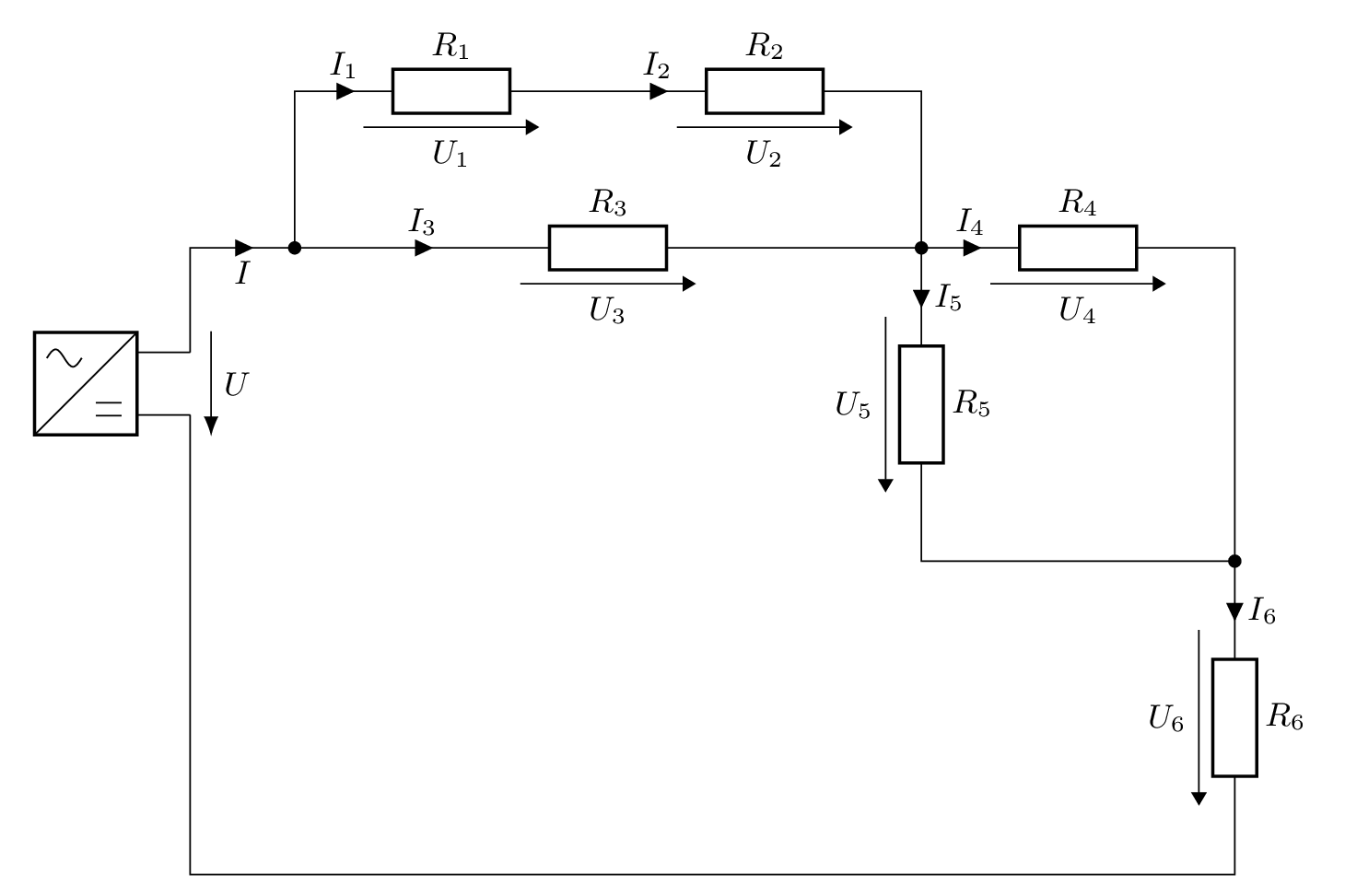
Notiere, welche Widerstände parallel zueinander sind und welche Widerstände in Reihe sind und berechne die gesuchten Größen.
geg:

\(U=230\ V\)
\(R_1=380\ m\Omega\)
\(R_2=790\ m\Omega\)
\(R_3=12\ \Omega\)
\(R_4=1,2\ \Omega\)
\(R_5=6,8\ \Omega\)
\(R_6=330\ \Omega\)

ges:

\(R_\mathrm{ges}\)
Spannungen \(U, U_1, U_2, U_3, U_4, U_5, U_6\)
Ströme \(I_1, I_2, I_3, I_4, I_5, I_6\)

Lös:
\(R_7=R_1+R_2=1,17\ \Omega\)
\(R_8=R_7||R_3=1,07\ \Omega\)
\(R_9=R_4||R_5=1,02\ \Omega\)
\(R_\mathrm{ges}=R_8+R_9+R_6=1,07\ \Omega+1,02\ \Omega+330\ \Omega=332,09\ \Omega\)
\(I=692,58\ mA\)
\(U_6=228,55\ V\)
\(U_9=706,43\ mV=U_4=U_5\)
\(U_8=741,06\ mV=U_3\)
\(I_4=588,70\ mA\)
\(I_5=103.89\ mA\)
\(I_3=61,76\ mA\)
\(I_7=633,39\ mA\)
\(U_1=240,68\ mV\)
\(U_2=500,38\ mV\)

Aufgabe 5

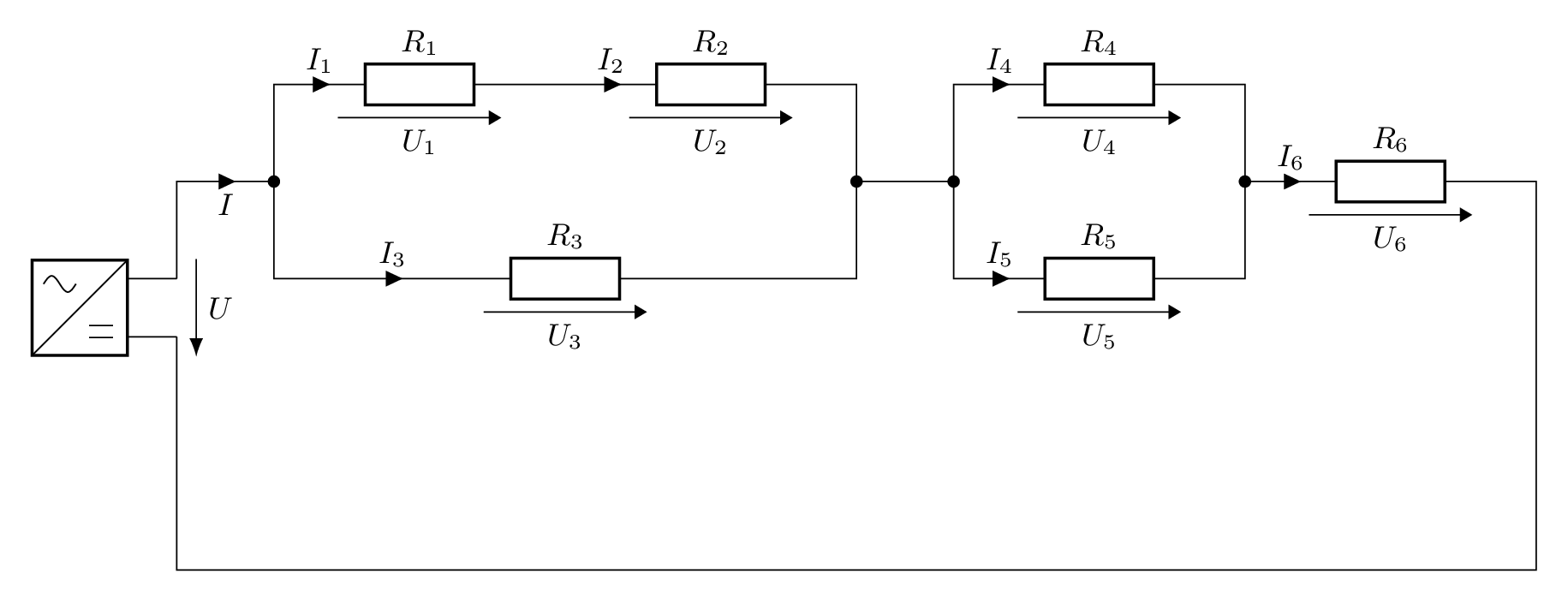
Notiere, welche Widerstände parallel zueinander sind und welche Widerstände in Reihe sind und berechne die gesuchten Größen.
geg:

\(I=2\ A\)
\(R_1=100\ \Omega\)
\(R_2=1\ k\Omega\)
\(R_3=24\ \Omega\)
\(R_4=2,3\ M\Omega\)
\(R_5=68\ m\Omega\)
\(R_6=57\ \Omega\)

ges:

\(R_\mathrm{ges}\)
Spannungen \(U, U_1, U_2, U_3, U_4, U_5, U_6\)
Ströme \(I_1, I_2, I_3, I_4, I_5, I_6\)

Lös:
\(R_7=R_1+R_2=1,10\ k\Omega\)
\(R_8=R_7||R_3=23,44\ \Omega\)
\(R_9=R_4||R_5=68\ m\Omega\)
\(R_\mathrm{ges}=R_8+R_9+R_6=23,44\ \Omega+68\ m\Omega+57\ \Omega=80,51\ \Omega\)
\(U=161,02\ V\)
\(U_6=114\ V\)
\(U_9=136\ mV=U_4=U_5\)
\(U_8=46,88\ V=U_3\)
\(I_4=59,13\ nA\)
\(I_5=2\ A\)
\(I_3=1,95\ A\)
\(I_7=42,62\ mA\)
\(U_1=4,26\ V\)
\(U_2=42,62\ V\)

Aufgabe 6

Berechne für folgendes Schaltbild

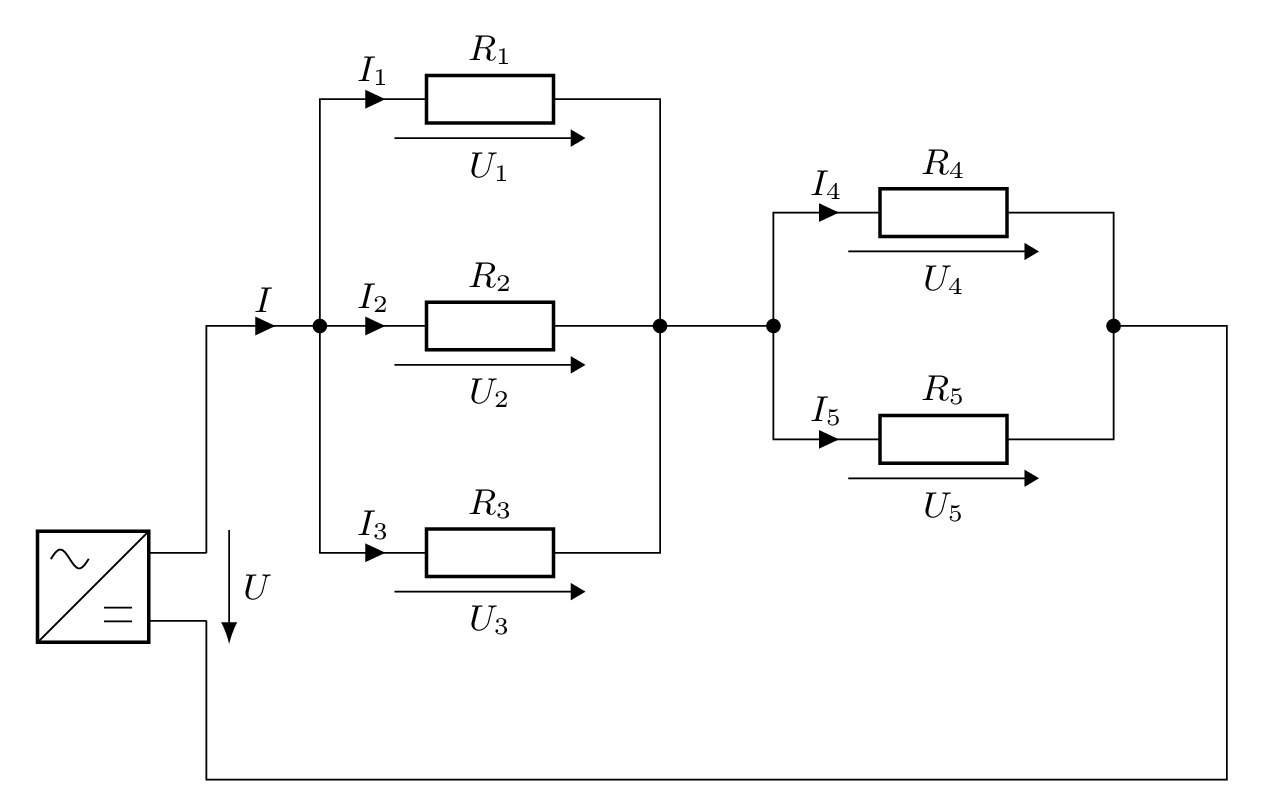
die gesuchten Werte.
geg:

\(U=15\ V\)
\(R_1=100\ \Omega\)
\(R_2=220\ \Omega\)
\(R_3=330\ \Omega\)
\(R_4=220\ \Omega\)
\(R_5=680\ \Omega\)

ges:

\(R_\mathrm{ges}\)
Spannungen: \(U_1, U_2, U_3, U_4, U_5\)
Ströme: \(I, I_1, I_2, I_3, I_4, I_5\)

Lös:
\(R_6=R_1||R_2=68,75\ \Omega\)
\(R_7=R_6||R_3=56,90\ \Omega\)
\(R_8=R_4||R_5=166,22\ \Omega\)
\(R_\mathrm{ges}=R_7+R_8=56,90\ \Omega+166,22\ \Omega=223,12\ \Omega\)
\(I=67,23\ mA\)
\(U_7= 3,83\ V=U_1=U_2=U_3\)
\(U_8= 11,18\ V=U_4=U_5\)
\(I_1=38,3\ mA\)
\(I_2=17,41\ mA\)
\(I_3=11,61\ mA\)
\(I_4=50,82\ mA\)
\(I_5=16,44\ mA\)

Hausaufgabe

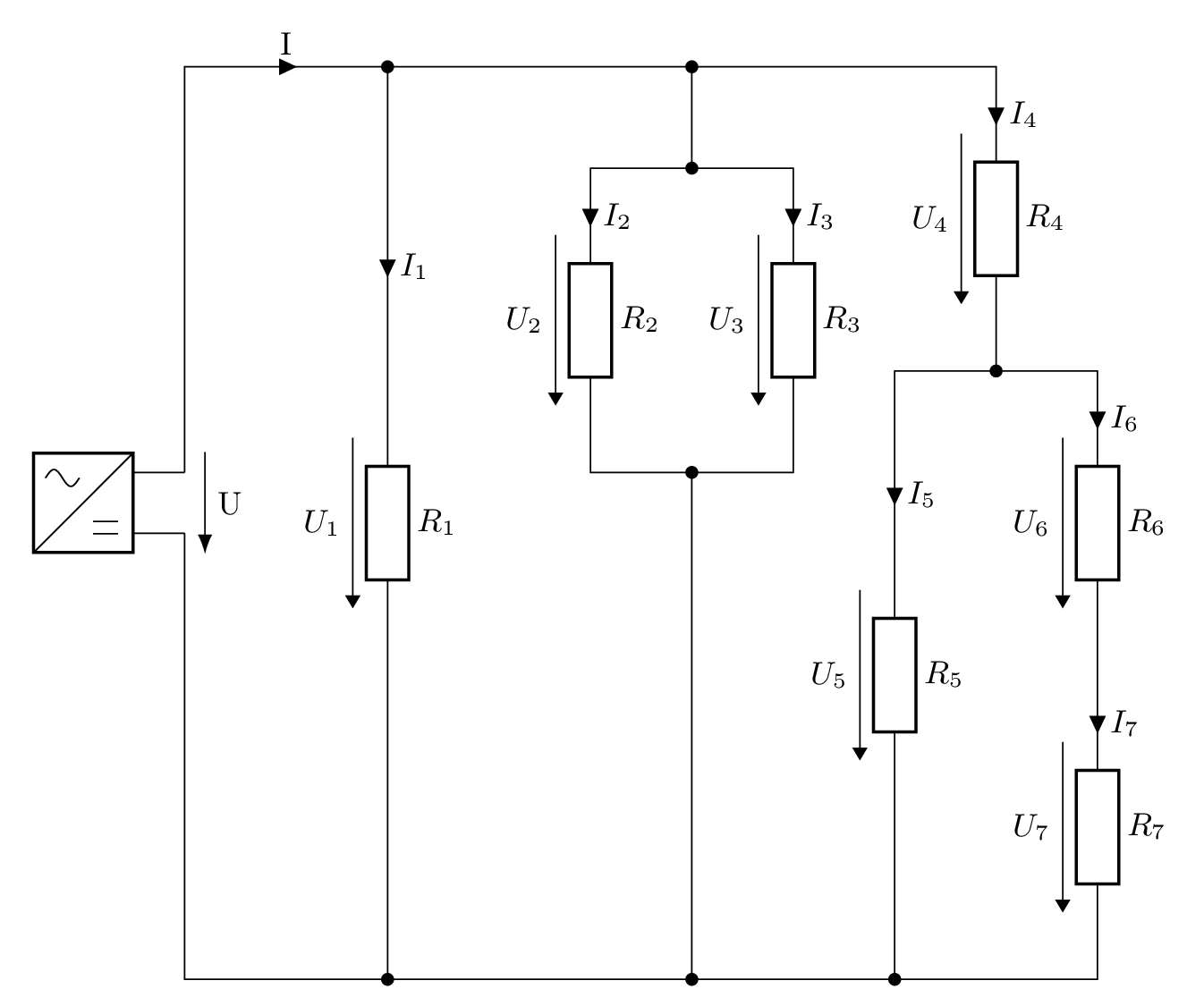
Notiere, welche Widerstände parallel zueinander sind und welche Widerstände in Reihe sind und berechne die gesuchten Größen.
geg:

\(U=12\ V\)
\(R_1=12\ \Omega\)
\(R_2=147\ \Omega\)
\(R_3=24\ \Omega\)
\(R_4=10\ \Omega\)
\(R_5 = 1,2\ M\Omega\)
\(R_6 = 7\ \mu\Omega\)
\(R_7 = 14\ m\Omega\)

ges:

\(R_\mathrm{ges}\)
Ströme: \(I, I_1, I_2, I_3, I_4, I_5, I_6, I_7\)
Spannungen: \(U_1, U_2, U_3, U_4, U_5, U_6, U_7\)

Lös:
\(U=U_1=U_2=U_3=12\ V\)
\(R_8=R_6+R_7=14,007\ m\Omega\)
\(R_9=R_5||R_8=14,007\ m\Omega\)
\(R_{10}=R_4+R_9=10,01\ \Omega\)
\(R_\mathrm{ges}=R_1||R_2||R_3||R_{10}=4,32\ \Omega\)
\(I=2,78\ A\)
\(I_1=1\ A\)
\(I_2=81,63\ mA\)
\(I_3=500\ mA\)
\(I_{10}=1,20\ A=I_4\)
\(U_4=12\ V\)
\(U_9=U_5=U_8=16,81\ mV\)
\(I_5=140\ \mu A\)
\(I_6=I_7=1,2\ A\)
\(U_6=8,4\ \mu V\)
\(U_7=16,8\ mV\)